Solving systems of inequalities has an interesting application--it
allows us to find the minimum and maximum values of quantities with
multiple constraints.
First, assign a variable ( x or y ) to each quantity that is being solved for. Write an equation for the quantity that is being maximized or minimized (cost, profit, amount, etc.). This is that maximization or minimization equation. Next, write each constraint as an inequality. Number each inequality and graph the system, numbering each line on the graph as its corresponding inequality.
You should now have a shaded solution region with several "corners." Each corner is the intersection of two constraint inequalities. Find the coordinates of the corners by solving the systems of intersecting equations.
Plug the coordinates of the corners into the maximization/minimization equation. The coordinates that give the largest or smallest value for this equation (depending on what the problem is looking for) are the solution to the problem.
There are three quantities that we are often asked to maximize and minimize in linear programming problems. Revenue is the total amount of money taken in, cost is the total amount of money spent, and profit is the revenue minus the cost, or the total amount of money gained.
Example: Jimmy is baking cookies for a bake sale. He is making chocolate chip and oatmeal raisin cookies. He gets 25 cents for each chocolate chip cookie and 30 cents for each oatmeal raisin cookie. He cannot make more than 500 cookies of each kind, and he cannot make more than 800 cookies total. He must make at least one-third as many chocolate chip cookies as oatmeal raisin cookies. How many of each kind of cookie should he make to get the most money?
Variables: x = number of chocolate chip cookies (in hundreds)
y = number of oatmeal raisin cookies (in hundreds) Maximization equation: Profit = 25x + 30y
Constraints:
1. x≤5 2. y≤5 3. x + y≤8 4. x≥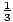 y
y
Graph:
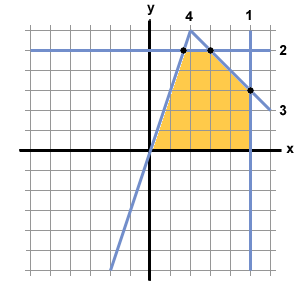
Corners:
Thus, the x and y values which maximize the profit are (x, y) = (3, 5) . Jimmy should bake 300 chocolate chip cookies and 500 oatmeal raisin cookies.
Example 2; Clive has decided that as a fund-raising activity he will make and sell candles. He has decided to make two types of candle, a plain one, and a scented one. Each candle requires 200g of wax and Clive has bought enough ingredients to make a total of 1.6kg of wax. His idea is to make the scented candles tall and thin, and the plain candles shorter and fatter. This means that the length of wick required for a scented candle is 200mm but only 100mm is needed for a plain candle. Clive only has 1m of wick to use. Clive has worked out from a survey that he won’t be able to sell more scented candles than double the number of plain candles plus three.
First, assign a variable ( x or y ) to each quantity that is being solved for. Write an equation for the quantity that is being maximized or minimized (cost, profit, amount, etc.). This is that maximization or minimization equation. Next, write each constraint as an inequality. Number each inequality and graph the system, numbering each line on the graph as its corresponding inequality.
You should now have a shaded solution region with several "corners." Each corner is the intersection of two constraint inequalities. Find the coordinates of the corners by solving the systems of intersecting equations.
Plug the coordinates of the corners into the maximization/minimization equation. The coordinates that give the largest or smallest value for this equation (depending on what the problem is looking for) are the solution to the problem.
There are three quantities that we are often asked to maximize and minimize in linear programming problems. Revenue is the total amount of money taken in, cost is the total amount of money spent, and profit is the revenue minus the cost, or the total amount of money gained.
Example: Jimmy is baking cookies for a bake sale. He is making chocolate chip and oatmeal raisin cookies. He gets 25 cents for each chocolate chip cookie and 30 cents for each oatmeal raisin cookie. He cannot make more than 500 cookies of each kind, and he cannot make more than 800 cookies total. He must make at least one-third as many chocolate chip cookies as oatmeal raisin cookies. How many of each kind of cookie should he make to get the most money?
Variables: x = number of chocolate chip cookies (in hundreds)
y = number of oatmeal raisin cookies (in hundreds) Maximization equation: Profit = 25x + 30y
Constraints:
1. x≤5 2. y≤5 3. x + y≤8 4. x≥
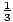 y
y
Graph:

Graph of Constraints
Corners:
1 and 3: x = 5 , x + y = 8 . (x, y) = (5, 3) . 2 and 3: y = 5 , x + y = 8 . (x, y) = (3, 5) . 2 and 4: y = 5 , x =Plug into maximization equation:y . (x, y) = (
, 5) .
(5, 3)âá’Profit = 25(5) + 30(3) = 215 . (3, 5)âá’Profit = 25(3) + 30(5) = 225 . (, 5)âá’Profit = 25(
) + 30(5) = 191.67 .
Thus, the x and y values which maximize the profit are (x, y) = (3, 5) . Jimmy should bake 300 chocolate chip cookies and 500 oatmeal raisin cookies.
Example 2; Clive has decided that as a fund-raising activity he will make and sell candles. He has decided to make two types of candle, a plain one, and a scented one. Each candle requires 200g of wax and Clive has bought enough ingredients to make a total of 1.6kg of wax. His idea is to make the scented candles tall and thin, and the plain candles shorter and fatter. This means that the length of wick required for a scented candle is 200mm but only 100mm is needed for a plain candle. Clive only has 1m of wick to use. Clive has worked out from a survey that he won’t be able to sell more scented candles than double the number of plain candles plus three.
If he is going to sell the candles at £3 for a scented candle and
£2 for a plain, how many of each should he make so that he raises
the most money possible?
The first thing that we must do is define our variables:
Let be
the number of plain candles made.
be
the number of plain candles made.
Let be
the number of scented candles made.
be
the number of scented candles made.
Let
Let be
the income from selling the candles.
be
the income from selling the candles.
Having defined the variables we can construct our constraint
inequalities using the information provided in the question. These
describe the conditions that will restrict the number of candles that
we can make.
The first constraint relates to the mass of wax available. 200g is
required for each candle, and the total available is 1.6kg.
Converting to consistent units and writing as an inequality, then
simplifying we get:
The second constraint is given by the amount of wick available and
required. 100mm is needed for each plain candle and 200mm is needed
for each scented candle. 1m is available. As with the first
constraint, we make sure the units are consistent, then write as an
inequality and simplify.
The final constraint is that Clive won’t be able to sell more
scented candles than double the number of plain candles plus three.
Although slightly complicated this constraint can be written as
follows:
Objective Function
Having constructed all of our constraint inequalities the only
thing left for us to do before solving the problem is to generate an
objective function. This is created from the information that tells
us what we are to optimise (usually make biggest or smallest). In
this case, we need to maximise income with each scented candle
selling at £3 and each plain candle selling at £2. The objective
function will be:
This problem can be solved graphically by constructing the graph
below. Using the inequalities already constructed,
and drawing them on a graph gives usthe diagram below.

Using the coordinates found at the vertices in the objective
function, we can work out which combination of scented and plain
candles will give the greatest income,
| 0 | 3 | 2 × 0 + 3 × 3 |
| £9 | ||
| 0.8 | 4.6 | 2 × 0.8 + 3 × 4.6 |
| £15.4 | ||
| 6 | 2 | 2 × 6 + 3 × 2 |
| £18 | ||
| 8 | 0 | 2 × 8 + 3 × 0 |
| £16 |
As you can see, the highest income can be achieved when 6 plain
candles and 2 scented candles are sold. This will give an income of
£18. Alternatively, we could plot the objective function for a
certain level of income, to give the line l-1 in the diagram above,
and move this line out and up (since we are trying to maximize the
income. This process gives us the lines l-2 and l-3 . The line is
just about to leave the viable region at the point with coordinate
(6,2), and this gives the income 2 × 6 + 3 × 2=£18 as before.







No comments:
Post a Comment