What are Forces?
A force results from the interaction between two objects. A force can be defined as a push or a pull which acts upon an object as a result of its interaction with another object.
When one object exerts a force on another
object it always experiences an equal opposing force in return from the
object it exerted the force on. Or in other words when two objects
interact, the forces they exert on one another are equal and opposite.
These forces are referred to as the action and reaction forces.
Forces are measured in units called newtons (N).
The unit is named after the famous physicists Sir Isaac Newton
(1642-1727) who Laws of Motion are instrumental in understanding the
effects of forces.
Examples of forces
Weight
Weight is the force of gravity, which is
the pull of the Earth on an object. To understand the force of gravity
the concept of mass needs to be understood as well.
The mass of an object is the amount of
matter it contains. Thus mass is a measure of how much stuff is in an
object. Mass is measured in kilograms (kg) and is the same no matter
where the object is located in the universe. For example and object of
mass 10kg on the Earth will have the same mass of 10kg on the moon or
anywhere else in the universe. Weight on the other hand is a measure of
the pull of a planet i.e. Earth on the stuff contained in the object.
The direction of the force of gravity is downwards towards the centre
of the Earth.
As mentioned earlier when two objects
interact they exert equal and opposite forces. The force that opposes
the force of gravity in called the Normal Force. This is equal to the
force of gravity and acts in an upwards direction (opposite to the
downwards direction of the force of gravity). This is exerted by the
surface upon which the object is positioned on. Therefore the force of
gravity is the action force and the normal force is the reaction force.
| FREE BODY FORCE DIAGRAMS Free-body force diagrams are used to give a clear and simple indication of the effect of the forces acting on an object. In a free-body force diagram only the forces acting directly on the object are shown. The forces are represented by arrows, the direction of the arrow gives the direction of the force and the size of the arrow represents the size of the force. This assists the reader in determining the net force acting on the object. |
Friction
Frictional forces are the forces that
oppose or prevent motion. These forces are a result of the interaction
between the surfaces of two objects (more precisely due to the
attractions between the molecules of the surfaces in contact). The
reason why a football that is kicked eventually comes to rest is due to
the friction forces between the surface of the rolling ball and the
grass and air it is in contact with.
Magnetic Forces
This is the force produced by magnetic
materials which pulls or repels other materials. For example the
magnetic strip on a refrigerator door catch pulls the door to the
refrigerator frame to keep the door closed.
Newton’s Laws of Motion
The relationship between forces and motion were first fully explained by Sir Isaac Newton in the sixteenth century. Before explaining Newton’s laws of Motion it is important the term resultant force is understood.
Resultant Force
The resultant force on an object is the sum of all the individual forces acting on the object taking into account the direction in which they are acting. Therefore all the forces acting on an object may be replaced by a single force which has the same effect as all the original forces acting together.
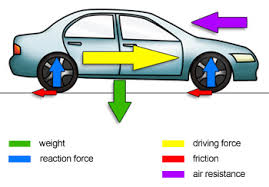
Newton’s First Law of Motion
Newton’s first law deals with objects at rest or those moving at constant speed.
Newton stated that if the resultant force on an object is zero then an object at rest will remain at rest and an object in motion will continue its motion in the same direction at constant speed.
This means that all objects have a natural tendency to keep on doing what they are doing. All objects have a reluctance to change their state of motion and require an unbalanced force to bring about a change
The reluctance or resistance for a mass to change its state of motion is referred to as inertia. This is why it is critical for drivers and passengers to wear seat belts. Passengers in cars possess a lot of inertia; if the car is forced to stop suddenly the passengers in the car will still move forward, the seat belts however exert large forces on the passengers to stop them.
The diagram below explains Newton’s first law of motion:

Newton’s Second Law of Motion
Newton’s first law deals with objects at rest or objects moving at constant velocity. His second law deals with the motion of accelerating and decelerating objects.
We know from everyday life examples such as pushing a car that if two people push a car on a flat road it will accelerate faster than if one person was pushing it. Thus, there is a relationship between the size of the force and the acceleration. We also know that it is easier for two people to push a small car than a large truck and for the same applied force the small car will accelerate faster than a large truck. Therefore there is also a relationship between mass and acceleration.
Experimentation proves that acceleration of a body is proportional to the force applied. This means that acceleration doubles when the force doubles or acceleration trebles when the force trebles, thus the greater the force the greater the acceleration. This relationship is represented as:

(where α represents "directly proportional to")
Experiments also show us if you keep the force constant and double the mass, the acceleration will halve. This means the acceleration is inversely proportional to the mass i.e. the greater the mass the less the acceleration.


Rearranging the above equation:

This equation gives the mathematical form of Newton’s second law of motion,
which states:
Provided the force is measured in newtons the second law can be written mathematically as:

The unit for measuring force is the newton. One newton is defined as:
The force which gives a mass of 1kg an acceleration of 1 m/s2

Force Acting in Free Fall
The force acting on an object in free fall is called its weight. The acceleration of the object is due to the force of gravity, therefore from Newton’s second law of motion we know;
Therefore,
F = m x g
(where “g” is acceleration due to gravity)
We know that force acting due to gravity is weight so,
Newton’s Third Law of Motion
Newton noticed that forces always come in pairs as a result of the interaction between two bodies and that the two forces were always equal in size and opposite in direction.
Momentum
Momentum is defined as the product of mass and velocity.

The unit for momentum is kilogram meters per second (kgm/s) and it is a vector quantity as it has both size and direction. The direction is given by the velocity (velocity = speed in a particular direction).
Thus, the momentum of an object depends on
its mass and its velocity. A 5000kg van travelling with a velocity of
6m/s will have a greater momentum than a 2000kg car travelling at the
same velocity of 6m/s. However, a 2000kg car travelling at a velocity
of 20m/s will have a greater momentum than the 5000kg van travelling at
6m/s.
From Newton’s second laws we know that:

And that the acceleration is the change in velocity by the time taken:

By substituting the value of “a” into the force equation it gives:



The above equation can be written as:
This equation confirms that when a resultant force acts on
an object it will cause a change of momentum in the direction of the
force and the size of the change depends on the size of the force and
the time for which it acts.
This can be explained by considering a sportsman or sportswoman striking a ball. A good sportsperson will always follow through when playing a shot. This means the force is applied for a longer time and so a greater change in momentum can be achieved for a given force.
Let’s consider the following example. A batsman strikes a cricket ball of mass 0.15kg accelerating it from 10m/s to 25m/s. The illustration below shows the force required when the bat acts on the ball for 1/100th of a second and for 1/10th of a second.
.Seat belts, airbags and crumple zones in cars also make use of this
concept. During a car accident the seat belt is designed to stretch
slightly, thereby increasing its time of contact with the wearer. This
reduces the force of the impact on the seat belt wearer. Crumple zones
in vehicles also increase the length of time of impact with a colliding
object thus reducing the force on the passengers.
This means that the change in momentum will be equal and opposite.
The principle of conservation of momentum is as follows:
For the principle of conversation to hold no external
forces must act on the colliding bodies as this would result in
momentum being added to the system.
The principle of conservation of momentum also applies to explosions. Explosions are the opposite to collisions. In explosions objects move apart. An example of this is a rocket. A rocket gains momentum by the controlled explosion of fuel as the hot exhaust gases move in one direction the rocket moves in the opposite direction. Thus the momentum of the hot exhaust gases equals the momentum of the rocket.
Friction

Resultant Force
The resultant force on an object is the sum of all the individual forces acting on the object taking into account the direction in which they are acting. Therefore all the forces acting on an object may be replaced by a single force which has the same effect as all the original forces acting together.
Newton’s First Law of Motion
Newton’s first law deals with objects at rest or those moving at constant speed.
Newton stated that if the resultant force on an object is zero then an object at rest will remain at rest and an object in motion will continue its motion in the same direction at constant speed.
This means that all objects have a natural tendency to keep on doing what they are doing. All objects have a reluctance to change their state of motion and require an unbalanced force to bring about a change
The reluctance or resistance for a mass to change its state of motion is referred to as inertia. This is why it is critical for drivers and passengers to wear seat belts. Passengers in cars possess a lot of inertia; if the car is forced to stop suddenly the passengers in the car will still move forward, the seat belts however exert large forces on the passengers to stop them.
The diagram below explains Newton’s first law of motion:
Newton’s Second Law of Motion
Newton’s first law deals with objects at rest or objects moving at constant velocity. His second law deals with the motion of accelerating and decelerating objects.
We know from everyday life examples such as pushing a car that if two people push a car on a flat road it will accelerate faster than if one person was pushing it. Thus, there is a relationship between the size of the force and the acceleration. We also know that it is easier for two people to push a small car than a large truck and for the same applied force the small car will accelerate faster than a large truck. Therefore there is also a relationship between mass and acceleration.
Experimentation proves that acceleration of a body is proportional to the force applied. This means that acceleration doubles when the force doubles or acceleration trebles when the force trebles, thus the greater the force the greater the acceleration. This relationship is represented as:
(where α represents "directly proportional to")
Experiments also show us if you keep the force constant and double the mass, the acceleration will halve. This means the acceleration is inversely proportional to the mass i.e. the greater the mass the less the acceleration.
It is important to note that the acceleration is parallel to the force applied.
Combing these two results we get:Rearranging the above equation:
This equation gives the mathematical form of Newton’s second law of motion,
which states:
| The acceleration of an object is inversely proportional to the mass of the object and directly proportion to the force acting on the object |
Provided the force is measured in newtons the second law can be written mathematically as:
The unit for measuring force is the newton. One newton is defined as:
The force which gives a mass of 1kg an acceleration of 1 m/s2
The animation below explains Newton’s second law of motion:
Force Acting in Free Fall
The force acting on an object in free fall is called its weight. The acceleration of the object is due to the force of gravity, therefore from Newton’s second law of motion we know;
F = m x a
Acceleration due to gravity is represented by “g” and is equal to 9.8m/s2.Therefore,
F = m x g
(where “g” is acceleration due to gravity)
We know that force acting due to gravity is weight so,
W = m x g
Newton noticed that forces always come in pairs as a result of the interaction between two bodies and that the two forces were always equal in size and opposite in direction.
In his third law Newton states:
| If body A exerts a force on body B, then body B exerts a force on body A that is equal in size but opposite in direction. |
Momentum is defined as the product of mass and velocity.
The unit for momentum is kilogram meters per second (kgm/s) and it is a vector quantity as it has both size and direction. The direction is given by the velocity (velocity = speed in a particular direction).
From Newton’s second laws we know that:
And that the acceleration is the change in velocity by the time taken:
By substituting the value of “a” into the force equation it gives:
The above equation can be written as:
Resultant Force x time taken = change in momentum
This can be explained by considering a sportsman or sportswoman striking a ball. A good sportsperson will always follow through when playing a shot. This means the force is applied for a longer time and so a greater change in momentum can be achieved for a given force.
Let’s consider the following example. A batsman strikes a cricket ball of mass 0.15kg accelerating it from 10m/s to 25m/s. The illustration below shows the force required when the bat acts on the ball for 1/100th of a second and for 1/10th of a second.
Conservation Of Momentum
We know from the equation mentioned in the section above that when a force acts on a body for a time it results in a change of momentum. When two bodies collide they exert a force over the same period of time which results in a change in momentum. From Newton’s third law we know if object A exerts a force on object B then object B exerts an equal and opposite force on object A.This means that the change in momentum will be equal and opposite.
The principle of conservation of momentum is as follows:
Total momentum before collision = total momentum after collision
The principle of conservation of momentum also applies to explosions. Explosions are the opposite to collisions. In explosions objects move apart. An example of this is a rocket. A rocket gains momentum by the controlled explosion of fuel as the hot exhaust gases move in one direction the rocket moves in the opposite direction. Thus the momentum of the hot exhaust gases equals the momentum of the rocket.
Friction
Friction is defined as a force that opposes motion.
When two objects are brought into contact
the molecules from the surface of one object get very close to the
molecules on the surface of the other object. This results in forces of
attraction between the molecules and this must be overcome so that one
surface can move over the other.
Objects moving through fluids such
as air or water also encounter frictional forces which reduce their
motion. This is known as drag.
Friction prevents objects from moving or
slows them down. It also causes wear on surfaces as they rub against
each other and generates heat. Thus energy is wasted in overcoming
friction.
Reducing friction
Lubrication
Oil is used as a lubricant and provides a thin layer of liquid which separates the moving surfaces.Bearings
Ball bearings reduce frictions by making the moving surface roll rather than slide.Streamlining
By designing the object to allow the easy
flow of fluid around it (streamlining) as is done for rockets and
racing cars the drag can be reduced considerably.
Uses of friction
Although in a lot of cases friction is a
hindrance but it is also very essential. In order to walk we depend on
the friction between the soles of our feet or shoes and the ground. The
tyres and brakes on vehicles depend on friction to stop, slow down and
start moving. It is the air resistance or drag that slows down a
parachute.
Stopping Distance
Cars rely on friction at the brakes and tyres in order to stop.
The total distance a car requires to stop
is called the total stopping distance. This is the sum of the distance
covered in the time it takes for the driver to react known as the thinking distance and the distance the car travels before coming to rest after the brakes are pressed called the braking distance.
Total stopping distance = thinking distance + braking distance
The diagram below gives the shortest stopping distances for a car on a dry road with good brakes and tyres.
From the diagram a clear pattern can be
seen between the velocity of the car and the total stopping distance.The
average reaction time of a driver is about 0.7s as the velocity of the
car increases so will the thinking distance from the relationship;
Distance travelled = velocity x reaction time
The braking distances increases because at a
faster velocity the car possesses more kinetic energy. This energy has
to be transferred to the brakes; this is transferred as heat and is
the reason why brakes become hot. The relationship between velocity and
kinetic energy is,
Kinetic Energy (Joules) = ½ x mass x velocity2
Therefore if the car travels three times
the velocity it has 9 times the kinetic energy which means the braking
distance will be nine times longer.
Factors affecting the total stopping distance
The driver’s reaction time
The thinking distance depends on the
driver’s reaction time. Reactions are strongly influenced by the state
of the mind. Thus, a driver under the influence of a drug such as
alcohol will have a much reduced reaction time which will increase the
thinking distance. Tiredness and fatigue also influence reaction time. A
tired driver will react a lot slower than an alert driver.
Velocity
As illustrated in the chart above the
braking distance increases with velocity. This is explained by the
relationship between kinetic energy and velocity. The greater the
velocity the greater the kinetic energy the brakes have to transfer.
Mass
The mass of the vehicle is also related to kinetic energy in the relationship;
Kinetic Energy (Joules) = ½ x mass x velocity2
The greater the mass the greater the kinetic energy, thus a heavier car will require a longer braking distance.
Road Surface
Friction between the car tyres and the road
surface stop it from skidding and sliding. On a wet or icy road
surface the contact between the tyres and the road is considerably
reduced. If the driver brakes hard the car will skid therefore the
driver needs to apply a reduced force on the brakes increasing the
braking distance.
Tyre Condition
Tyres are designed with grooves which
channel the water away on wet roads in order to ensure contact of the
tyre is made with the road. If the tyres are worn the friction between
the road and tyres is reduced increasing braking distance.
Brake Condition
Worn brakes will take longer to transfer the kinetic energy of the car increasing the braking distance.







No comments:
Post a Comment